Dynamic Programming

 

A method for solving a complex problem by breaking it down into collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions.

 

'dynamic' was chosen by Bellman to capture the time varing aspect of the problems.

'programming' didn't refer to computer programming but to finding an optimal program n the same way.

 

It only works on problems with optimal substructure & overlapping subproblems

 

 

Overlapping  Subproblems

 

ex) Fibonacci sequence - Every number after the first two is the sum of the two preceding ones

break down one problem into smaller steps which often do in recursion.

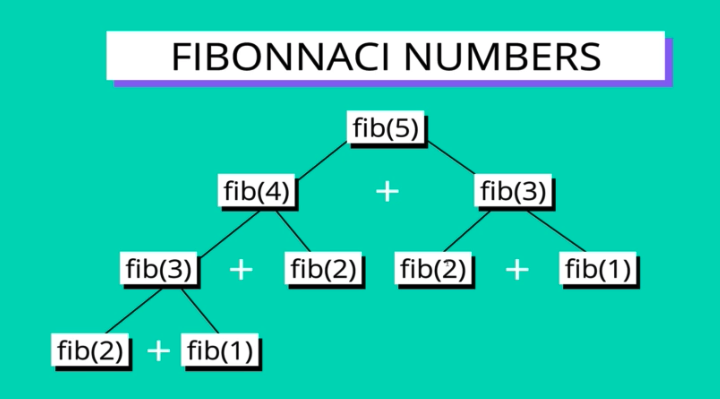
Overlapping problems means that we are repeating sub problem.

 

Optimal Substructure

 

A problem is said to have optimal substructure if an optimal solution can be constructed from optimal solution of its subproblems.

 

ex) the shortest path going from a start to an end.

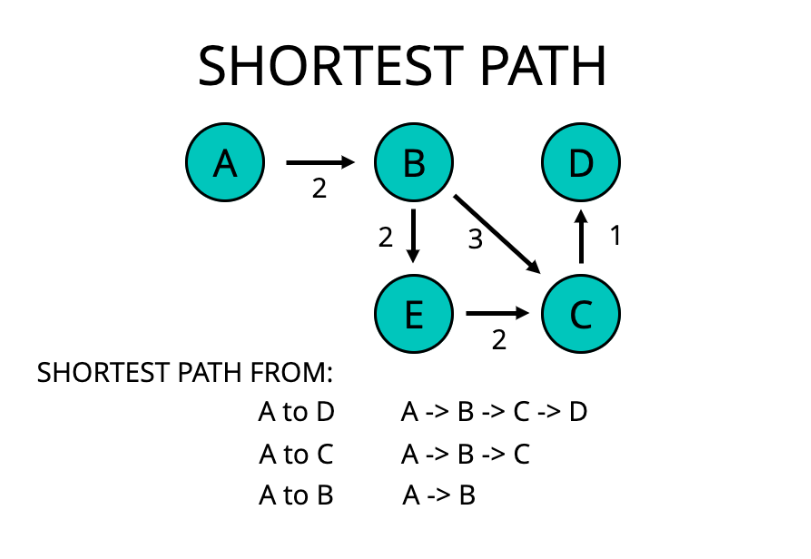
whatever the path is, any other point along that path also is going to be the shortest path from the starts to that point.

 

Writing a recursive solution & dynamic programming refactoring 

 

ex) Fibonnaci Numbers

we keep recursing down until we hit the base case.

 

// recursive solution.
// O(2^n)

function fib(n) {
  if(n <= 2) return 1;
  return fib(n-1) + fib(n-2);
}

 

Using past knowledge to make solving a futrure proble easier

 

Memoization

- storing the results of expensive function calls and returning the cached result when the same inputs occur again.

 

// a memo-ized solution
// O(n)

function fub(n, memo=[]) {
  if(memo[n] !== undefined) return memo[n];
  if(n <= 2) return 1;
 
  ver res = fib(n-2, memo) + fib(n-2, memo);
  memo[n] = res;
  return res;
}

looking up a value in an array is constant time.

 

Tabulation

- stroring the result of a previous result in a 'table' (array)

usually done using iterarion. better space complexity can be achieved.

 

// tabulated version
// O(n)
// better space complexity  

function fib(n) {
  if(n <= 2) return 1;
  var fibNums = [0,1,1];
  for(var i = 3; i<= n; i++) {
    fibNums[i] = fibNums[i-1] + fibNums[i-2];
  }
  return fibNums[n];
}