one of the most famous and widely used algorithms
the shortest path between the vertices.
Edsger Dijkstra, a Dutch programmer
Useful for
- GPS - finding fastest route
- Network Routing - finds open shortest path for data
- Biology - used to model the spread of viruses among humans
- Airline tickets - finding cheapest route to your destination
- Many other uses!
thr first thing is we need to do is adding a weight (associated value) to the graph.
class WeightedGraph {
constructor() {
this.adjacencyList = {};
}
addVertex(vertex) {
if(!this.adjacencyList[vertex]) this.adjacecyList[vertex] = [];
}
addEdge(vertex1, vertex2, weight) {
this.adjacencyList[vertex1].push({node:vertex2, weight});
this.adjacencyList[vertex2].push({node:vertex1, weight});
}
}
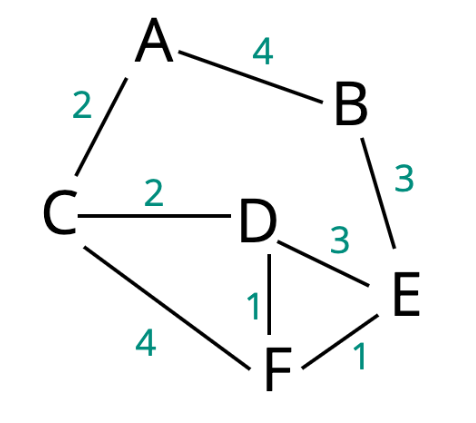
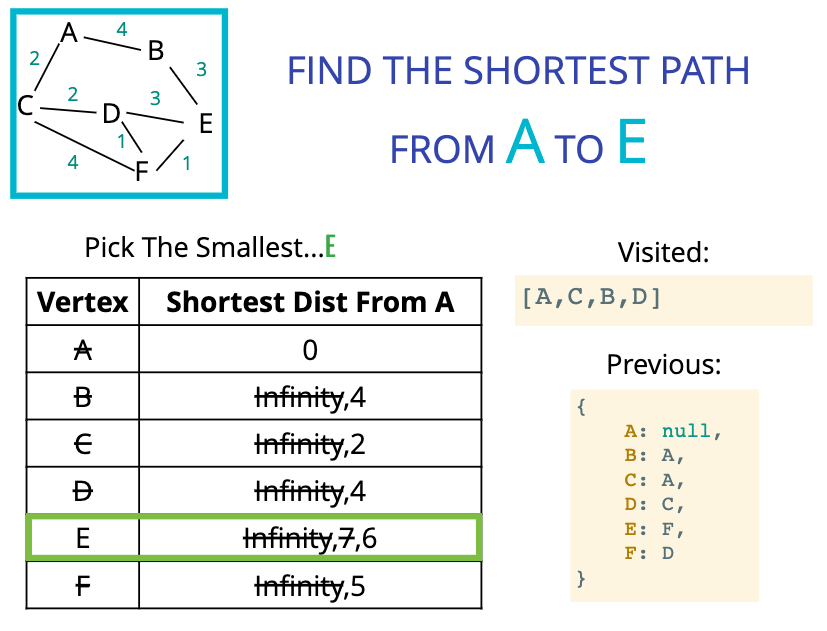
Find the shortest path from A to E
Dijkstra's algorithm works not only to give the shortest path between two nodes.
at the end, the way of implementing it, we'll have a data structure that gives the shortest path from A to all the nodes.
A priority queue how that played a role in the algorithm
to find the next smallest one to visit.
everytime you add something to it, you give it a priority.
and get the smallest out first.
class PriorityQueue {
constructor() {
this.values = [];
}
enqueue(val, priority) {
this.values.push({val, priority});
this.sort();
}
dequeue() {
return this.values.shift();
}
sort() {
this.values.sort((a,b) => a.priority - b.priority);
}
}
Dijkstra's Pseudocode
- This function should accept a starting and ending vertex
- Create an object (we'll call it distances) and set each key to be every vertex in the adjacency list with a value of infinity, except for the starting vertex which should have a value of 0.
- After setting a value in the distances object, add each vertex with a priority of Infinity to the priority queue, except the starting vertex, which should have a priority of 0 because that's where we begin.
- Create another object called previous and set each key to be every vertex in the adjacency list with a value of null
- Start looping as long as there is anything in the priority queue
- dequeue a vertex from the priority queue
- If that vertex is the same as the ending vertex - we are done!
- Otherwise loop through each value in the adjacency list at that vertex
- Calculate the distance to that vertex from the starting vertex
- if the distance is less than what is currently stored in our distances object
- update the distances object with new lower distance
- update the previous object to contain that vertex
- enqueue the vertex with the total distance from the start node
class WeightedGraph {
constructor() {
this.adjacencyList = {};
}
addVertex(vertex) {
if(!this.adjacencyList[vertex]) this.adjacecyList[vertex] = [];
}
addEdge(vertex1, vertex2, weight) {
this.adjacencyList[vertex1].push({node:vertex2, weight});
this.adjacencyList[vertex2].push({node:vertex1, weight});
}
dijkstra(start, finish) {
const nodes = new PriorityQueue();
const distances = {};
const previous = {};
let smallest;
let path = []; // to return at the end
// build up initial state
for(let vertex in this.adjacencyList) {
if(vertex == start) {
distances[vertex] = 0;
nodes.enqueue(vertex, 0);
} else {
distances[vertex] = infinity;
nodes.enqueue(vertex, Infinity);
}
previous[vertex] = null;
}
// as long as there is something to visit
while(nodes.values.length) {
smallest = nodes.dequeue().val;
if(smallest == finish) {
// we are done.
// build up path to return at end
while(previous[smallest]) {
path.push(smallest);
smallest = previous[smallest];
}
break;
}
if(smallest || distances[smallest] !== Infinity) {
for(let neighbor in this.adjacencyList[smallest]) {
// find neighboring node
let nextNode = this.adjacencyList[smallest][neighbor];
// calculate new distance to neighboring node
let candidate = distances[smallest] + nextNode.weight;
let nextNeighbor = nextNode.node;
if(candidate < distances[nextNode.node]) {
// updateing new smallest distance to neighbor
distances[nextNeighbor] = candidate;
// updating previous - how we got to neighbor
previous[nextNeighbor] = smallest;
// enqueue in priority queue with new priority
nodes.enqueue(nextNeighbor, candidate);
}
}
}
}
return path.concat(smallest).reverse();
}
}
Using a binary heap priority queue is much faster than using a priority queue above.
'Javascript > Algorithms' 카테고리의 다른 글
| Dynamic Programming (0) | 2021.08.16 |
|---|---|
| Merge Sort (0) | 2021.01.19 |
| Insertion Sort (0) | 2021.01.03 |
| Selection Sort (0) | 2021.01.03 |
| Bubble Sort (0) | 2020.12.27 |
